---> For French version of this article, click here
I'm a Machine Learning engineer and I use libraries like Tensorflow and Pytorch in my work to train my neural networks. And it's been a while since I wanted to write the simplest piece of code to perform what is called automatic differentiation which is at the heart of neural network training.
In this article, I will try to iteratively build the simplest code to calculate derivatives automatically on scalars.
In the following Python code, the sum between x and y will be performed and the result (8) will be assigned to the variable z. After the assignment, the z variable keeps no track of the variables used, so there is no way to automatically update the value of z if the value of x or y changes. Even less possible to understand the link between each variable to calculate a derivative automatically.
x = 3
y = 5
z = x + y
The Tensor class
The idea is to create a new type, a Tensor, which will allow us to do symbolic calculation on our variables.
Let's start by creating a Tensor class where the addition operation is redefined.
import numpy as np
class Tensor:
def __init__(self, value=None):
self.value = value
def __repr__(self):
return f"T:{self.value}"
def __add__(self, other):
t = Tensor(value = self.value + other.value)
return t
x = Tensor(3)
y = Tensor(5)
z = x + y
print(x, y)
print(z)
# Out:
# T:3 T:5
# T:8
In this example, we create a Tensor class that can store a value, and we redefine addition to create a new Tensor when we perform an addition between two Tensors. There is no symbolic computation mechanism yet that will allow z to have a trace that it is the result of the addition between x and y.
We will add this behavior by using a binary tree. Each tensor will be able to contain the other two tensors and the operation that produced it. To do this, we introduce the Children tuple which will contain these three pieces of information.
import numpy as np
from collections import namedtuple
Children = namedtuple('Children', ['a', 'b', 'op'])
class Tensor:
def __init__(self, value=None, children=None):
self.value = value
self.children = children
def forward(self):
if self.children is None:
return self
# compute forward pass of children in the tree
a = self.children.a.forward()
b = self.children.b.forward()
# If values are set, let's compute the real value of this tensor
if a.value is not None and b.value is not None:
self.value = self.children.op(a.value, b.value)
return self
def __repr__(self):
return f"T:{self.value}"
def __add__(self, other):
c = Children(self, other, np.add)
t = Tensor(children=c)
return t.forward()
def __mul__(self, other):
c = Children(self, other, np.multiply)
t = Tensor(children=c)
return t.forward()
x = Tensor(3)
y = Tensor(5)
z1 = x + y
z2 = z1 * y
print(x, y)
print(z2)
# Out
# T:3 T:5
# T:40
Now a tensor, in addition to containing a numerical value, will contain the tuple children allowing it to keep track of the calculation. In this example, in addition to introducing the Children type, we have added the multiplication method to tensors. The forward method to the Tensor class has also been added to be able to execute the computation graph and compute the actual value of the tensors. The tensor z2 can be modeled by the following computation graph.
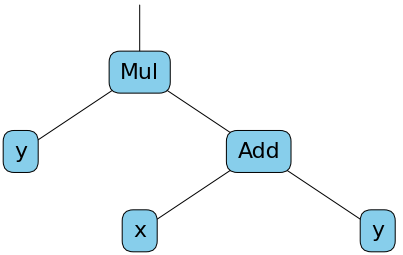
We can check that it works as expected by first creating the graph without specifying any values:
x = Tensor(None)
y = Tensor(None)
z1 = x + y
z2 = z1 * y
print(x, y)
print(z2)
# Out
# T:None T:None
# T:None
Then the values of the leaves of the tree (x and y) can be changed and the value of z2 calculated. The call to z2.forward() will cause the forward method of z and y to be called, and these calls will browse the graph to recursively calculate the value of z2.
x.value = 3
y.value = 5
print(z2.forward())
# Out
# T:40
Adding Automatic Differenciation
To add automatic differentiation to an arbitrary computation graph, we simply add the derivative for the basic operations supported by our Tensor class. Recursive calls to the grad function will traverse the computation graph and decompose a complex function to be derived into a combination of simple functions.
def grad(self, deriv_to):
# Derivative of a tensor with itself is 1
if self is deriv_to:
return Tensor(1)
# Derivative of a scalar with another tensor is 0
if self.children is None:
return Tensor(0)
if self.children.op is np.add: # (a + b)' = a' + b'
t = self.children.a.grad(deriv_to) + self.children.b.grad(deriv_to)
elif self.children.op is np.multiply: # (ab)' = a'b + ab'
t = self.children.a.grad(deriv_to) * self.children.b + \
self.children.a * self.children.b.grad(deriv_to)
else:
raise NotImplementedError(f"This op is not implemented. {self.children.op}")
return t
We can now derive z2 as a function of the variable of our choice:
print(x, y)
g = z2.grad(y)
print(g)
# Out
# T:3 T:5
# T:13
Here, g is not just a value, it is a new computational graph that represents the partial derivative of z2 as a function of y. Since the value of x and y was defined when grad was called, the value of g could be calculated. The calculation graph of g can be represented by this diagram:
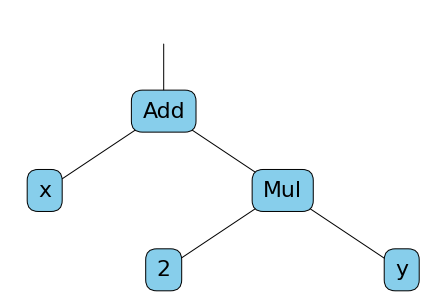
Literally $g = \frac{\partial z_2}{\partial y} = x + 2*y$, and when x and y are 3 and 5 respectively, then g is 13.
Enabling the Tensor class to handle more complex formulas
To be able to use more complex formulas, we will add more operations to the Tensor class. We add subtraction, division, exponential and negation (-x).
Here is the Tensor class in its final form:
class Tensor:
def __init__(self, value=None, children=None, name=None):
self.children = children
self.value = value
self.name = name
def forward(self):
if self.children is None:
return self
a = None
b = None
# compute forward pass of children in the tree
if self.children.a is not None:
a = self.children.a.forward()
if self.children.b is not None:
b = self.children.b.forward()
# If a has a specific value after forward pass
if a.value is not None:
# If the operation does not need a term b (like exp(a) for example)
# Use only a
if self.children.b is None:
self.value = self.children.op(a.value)
# Else if op needs a second term b and his value is not None after forward pass
elif b.value is not None:
self.value = self.children.op(a.value, b.value)
return self
def grad(self, deriv_to):
# Derivative of a tensor with itself is 1
if self is deriv_to:
return Tensor(1)
# Derivative of a scalar with another tensor is 0
if self.children is None:
return Tensor(0)
if self.children.op is np.add: # (a + b)' = a' + b'
t = self.children.a.grad(deriv_to) + self.children.b.grad(deriv_to)
elif self.children.op is np.subtract: # (a - b)' = a' - b'
t = self.children.a.grad(deriv_to) - self.children.b.grad(deriv_to)
elif self.children.op is np.multiply: # (ab)' = a'b + ab'
t = self.children.a.grad(deriv_to) * self.children.b + \
self.children.a * self.children.b.grad(deriv_to)
elif self.children.op is np.divide: # (a/b)' = (a'b - ab') / b²
t = (
self.children.a.grad(deriv_to) * self.children.b - \
self.children.a * self.children.b.grad(deriv_to)
) / \
(self.children.b * self.children.b)
elif self.children.op is np.exp: # exp(a)' = a'exp(a)
t = self.children.a.grad(deriv_to) * self.children.a.exp()
else:
raise NotImplementedError(f"This op is not implemented. {self.children.op}")
return t
def __repr__(self):
return f"T:{self.value}"
def __add__(self, other):
c = Children(self, other, np.add)
t = Tensor(children=c)
return t.forward()
def __sub__(self, other):
c = Children(self, other, np.subtract)
t = Tensor(children=c)
return t.forward()
def __mul__(self, other):
c = Children(self, other, np.multiply)
t = Tensor(children=c)
return t.forward()
def __truediv__(self, other):
c = Children(self, other, np.divide)
t = Tensor(children=c)
return t.forward()
def __neg__(self):
c = Children(Tensor(value=np.zeros_like(self.value)), self, np.subtract)
t = Tensor(children=c)
return t.forward()
def exp(self):
c = Children(self, None, np.exp)
t = Tensor(children=c)
return t.forward()
For each operation added to the Tensor class, the corresponding derivative has been included in the grad method. Also, we have modified forward to handle more cases, especially to handle operations that require only one term like exponential or negation.
Now let's create a more complex formula and derive it!
Let's try to derive $z$ :
$$z = \frac{12 - (x * e^{y})}{45 + x * y * e^{-x}}$$
We just have to write this equation using our Tensor class:
x = Tensor(3)
y = Tensor(5)
z = (Tensor(12) - (x * y.exp())) / (Tensor(45) + x * y * (-x).exp())
This will generate for the tensor z, the following computation graph:
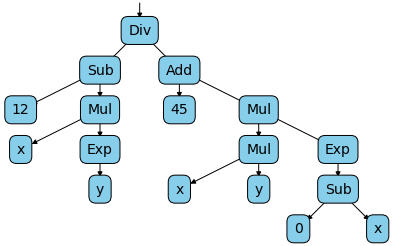
We can now easily calculate the partial derivative of z as a function of x and y with the following code:
print(z.grad(x)) # T:-3.34729777301069
print(z.grad(y)) # T:-9.70176956641438
This will generate the following two graphs:
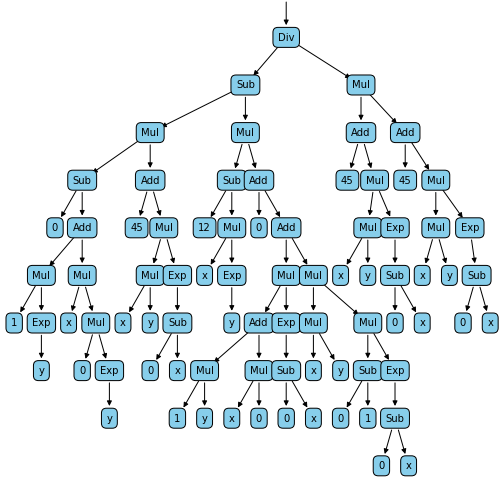
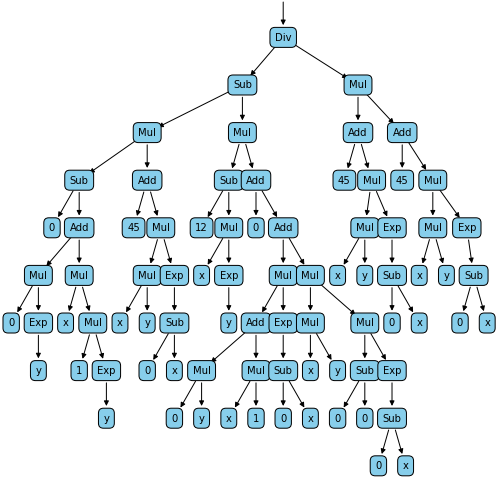
Finally, to check that our automatic derivation system works, we can compare the numerical calculation of our derivatives with the calculation done by the Sympy library:
import sympy as sym
xs = sym.Symbol('xs')
ys = sym.Symbol('ys')
zs = (12 - (xs * sym.exp(ys))) / (45 + ((xs * ys) * sym.exp(-xs)) )
d = zs.diff(ys)
print(zs.diff(xs).evalf(subs={xs:3, ys:5})) # -3.34729777301069
print(zs.diff(ys).evalf(subs={xs:3, ys:5})) # -9.70176956641438
The result obtained with the Sympy library is strictly the same as with our Tensor class !
Possible Improvements & Optimizations
We have just created the simplest automatic differentiation system that exists, and probably also the slowest. We can add more complex operations if we want, as long as we know how to derive them. As it is, this class can only handle scalars; for such a library to be most useful, one would have to add operations on arrays of arbitrary sizes.
Also, looking at the graphs, we can see that some optimizations are possible:
- If we are in a multiplication node and one of the two `children` is 0, we **should not explore further**. Because we know that whatever is multiplied by 0, will always be 0.
- When traversing the tree to perform a derivative with respect to a tensor `x`, if we are in a node that does not depend on `x` and whose children do not depend on `x`, we could stop the traversal at this step and **consider the current node as a constant**. This type of optimization could greatly improve the computational speed for graphs with many nodes and different variables.
- By looking at the graph we can see that some operations are repeated. We can imagine **to set up a cache** to avoid repeating the computations several times.
I hope this article has helped you understand how automatic differentiation is performed for neural network optimization and learning.
Feel free to give me your feedback in comments!