---> For English version of this article, click here
Je suis ingénieur Machine Learning et j'utilise dans mon travail des bibliothèques telles que Tensorflow et Pytorch pour entrainer mes réseaux de neurones. Et ça faisait un moment que je voulais écrire le bout de code le plus simple pour effectuer ce que l'on appelle la différenciation automatique qui est au coeur de l'apprentissage des réseaux de neurones.
Dans cet article, je vais essayer de construire de façon itérative le code le plus simple pour calculer des dérivées automatiquement sur des scalaires.
Dans le code Python suivant, la somme entre x et y va être effectuée et le résultat (8) va être assigné à la variable z. Après l'assignation, la variable z ne garde aucune trace des variables utilisées, pas moyen de mettre à jour automatiquement la valeur de z si celle de x ou y change. Encore moins possible de comprendre le lien entre chaque variable pour calculer une dérivée automatiquement.
x = 3
y = 5
z = x + y
La classe Tensor
Le principe va consister à créer un nouveau type, un Tensor, qui va nous permettre de faire du calcul symbolique sur nos variables.
Commençons par créer une classe Tensor où l'opération d'addition est redéfinie.
import numpy as np
class Tensor:
def __init__(self, value=None):
self.value = value
def __repr__(self):
return f"T:{self.value}"
def __add__(self, other):
t = Tensor(value = self.value + other.value)
return t
x = Tensor(3)
y = Tensor(5)
z = x + y
print(x, y)
print(z)
# Out:
# T:3 T:5
# T:8
Dans cet exemple, on créé une classe Tensor pouvant stocker une valeur, et on redéfinit l'addition pour créer un nouveau Tensor quand on effectue une addition entre deux Tensor. Il n'y a pas encore de mechanisme de calcul symbolique qui va permettre à z d'avoir une trace qu'elle est le résultat de l'addition entre x et y.
Nous allons ajouter ce comportement en utilisant un arbre binaire. Chaque tenseur va pouvoir contenir les deux autres tenseurs et l'opération qui l'a produite. Pour ça, on introduit le tuple Children qui va contenir ces trois informations.
import numpy as np
from collections import namedtuple
Children = namedtuple('Children', ['a', 'b', 'op'])
class Tensor:
def __init__(self, value=None, children=None):
self.value = value
self.children = children
def forward(self):
if self.children is None:
return self
# compute forward pass of children in the tree
a = self.children.a.forward()
b = self.children.b.forward()
# If values are set, let's compute the real value of this tensor
if a.value is not None and b.value is not None:
self.value = self.children.op(a.value, b.value)
return self
def __repr__(self):
return f"T:{self.value}"
def __add__(self, other):
c = Children(self, other, np.add)
t = Tensor(children=c)
return t.forward()
def __mul__(self, other):
c = Children(self, other, np.multiply)
t = Tensor(children=c)
return t.forward()
x = Tensor(3)
y = Tensor(5)
z1 = x + y
z2 = z1 * y
print(x, y)
print(z2)
# Out
# T:3 T:5
# T:40
Maintenant, un tenseur, en plus de contenir une valeur numérique, va contenir le tuple children lui permettant de garder une trace du calcul. Dans cet exemple, en plus d'avoir introduit le type Children, nous avons rajouté la méthode de multiplication sur les tenseurs. La méthode forward à la classe Tensor a également été ajoutée pour pouvoir exécuter le graphe de calcul et calculer la valeur réelles des tenseurs. Le tenseur z2 peut être modélisé par le graphe de calcul suivant.
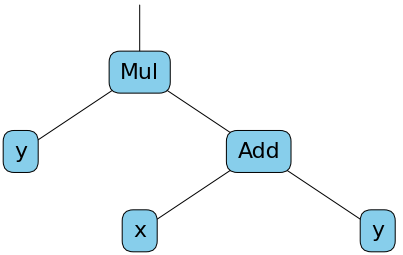
On peut vérifier que ça marche comme attendu en créant d'abord le graphe sans préciser de valeurs :
x = Tensor(None)
y = Tensor(None)
z1 = x + y
z2 = z1 * y
print(x, y)
print(z2)
# Out
# T:None T:None
# T:None
Puis les valeurs des feuilles de l'arbre (x et y) peuvent être changées et la valeur de z2 calculée. L'appel à z2.forward() va provoquer un appel la méthode forward de z et y, et ces appels vont permettre de descendre dans le graphe pour calculer récursivement la valeur de z2.
x.value = 3
y.value = 5
print(z2.forward())
# Out
# T:40
Ajouter la dérivation automatique
Pour ajouter la différenciation automatique à un graphe de calcul arbitraire, nous ajoutons simplement la dérivée pour les opérations de base supportées par notre classe Tensor. Des appels récursifs à la fonction grad traverseront le graphe de calcul et décomposeront une fonction complexe à dériver en une combinaison de fonctions simples.
def grad(self, deriv_to):
# Derivative of a tensor with itself is 1
if self is deriv_to:
return Tensor(1)
# Derivative of a scalar with another tensor is 0
if self.children is None:
return Tensor(0)
if self.children.op is np.add: # (a + b)' = a' + b'
t = self.children.a.grad(deriv_to) + self.children.b.grad(deriv_to)
elif self.children.op is np.multiply: # (ab)' = a'b + ab'
t = self.children.a.grad(deriv_to) * self.children.b + \
self.children.a * self.children.b.grad(deriv_to)
else:
raise NotImplementedError(f"This op is not implemented. {self.children.op}")
return t
On peut maintenant dériver z2 en fonction de la variable de notre choix:
print(x, y)
g = z2.grad(y)
print(g)
# Out
# T:3 T:5
# T:13
Ici, g n'est pas seulement une valeur, c'est un nouveau graphe de calcul qui représente la dérivée partielle de z2 en fonction de y. Comme la valeur de x et y était définie au moment de l'appel à grad, la valeur de g a pu être calculée. Le graphe de calcul de g peut être représenté par ce schéma :
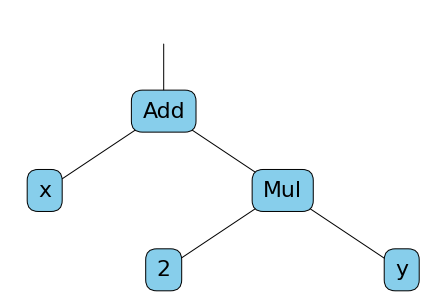
Littéralement $g = \frac{\partial z_2}{\partial y} = x + 2*y$, et lorsque x et y valent respectivement 3 et 5, alors g vaut 13.
Permettre à la classe Tensor de manipuler des formules plus complexes
Pour pouvoir utiliser des formules plus complexes, nous allons rajouter d'autres opérations à la classe Tensor. Nous ajoutons la soustraction, la division, l'exponentielle et la négation (-x).
Voici la classe Tensor dans sa forme finale :
class Tensor:
def __init__(self, value=None, children=None, name=None):
self.children = children
self.value = value
self.name = name
def forward(self):
if self.children is None:
return self
a = None
b = None
# compute forward pass of children in the tree
if self.children.a is not None:
a = self.children.a.forward()
if self.children.b is not None:
b = self.children.b.forward()
# If a has a specific value after forward pass
if a.value is not None:
# If the operation does not need a term b (like exp(a) for example)
# Use only a
if self.children.b is None:
self.value = self.children.op(a.value)
# Else if op needs a second term b and his value is not None after forward pass
elif b.value is not None:
self.value = self.children.op(a.value, b.value)
return self
# TODO: manage case when the two tensors are independant
def grad(self, deriv_to):
# Derivative of a tensor with itself is 1
if self is deriv_to:
return Tensor(1)
# Derivative of a scalar with another tensor is 0
if self.children is None:
return Tensor(0)
if self.children.op is np.add: # (a + b)' = a' + b'
t = self.children.a.grad(deriv_to) + self.children.b.grad(deriv_to)
elif self.children.op is np.subtract: # (a - b)' = a' - b'
t = self.children.a.grad(deriv_to) - self.children.b.grad(deriv_to)
elif self.children.op is np.multiply: # (ab)' = a'b + ab'
t = self.children.a.grad(deriv_to) * self.children.b + \
self.children.a * self.children.b.grad(deriv_to)
elif self.children.op is np.divide: # (ab)' = (a'b - ab') / b²
t = (
self.children.a.grad(deriv_to) * self.children.b - \
self.children.a * self.children.b.grad(deriv_to)
) / \
(self.children.b * self.children.b)
elif self.children.op is np.exp: # exp(a)' = a'exp(a)
t = self.children.a.grad(deriv_to) * self.children.a.exp()
else:
raise NotImplementedError(f"This op is not implemented. {self.children.op}")
return t
def __repr__(self):
return f"T:{self.value}"
def __add__(self, other):
c = Children(self, other, np.add)
t = Tensor(children=c)
return t.forward()
def __sub__(self, other):
c = Children(self, other, np.subtract)
t = Tensor(children=c)
return t.forward()
def __mul__(self, other):
c = Children(self, other, np.multiply)
t = Tensor(children=c)
return t.forward()
def __truediv__(self, other):
c = Children(self, other, np.divide)
t = Tensor(children=c)
return t.forward()
def __neg__(self):
c = Children(Tensor(value=np.zeros_like(self.value)), self, np.subtract)
t = Tensor(children=c)
return t.forward()
def exp(self):
c = Children(self, None, np.exp)
t = Tensor(children=c)
return t.forward()
Pour chaque opération ajoutée à la classe Tensor, la dérivée correspondante a été inclue dans la méthode grad. Également, nous avons modifié forward pour gérer plus de cas, notamment pour gérer les opérations qui ne nécéssitent qu'un terme comme l'exponentielle ou la négation.
Maintenant, créons une formule plus complexe et dérivons la !
Essayons de dériver $z$ :
$$z = \frac{12 - (x * e^{y})}{45 + x * y * e^{-x}}$$
Nous n'avons qu'à écrire cette équation en utilisant notre classe Tensor :
x = Tensor(3)
y = Tensor(5)
z = (Tensor(12) - (x * y.exp())) / (Tensor(45) + x * y * (-x).exp())
Ce qui va générer pour le tenseur z, le graphe de calcul suivant :
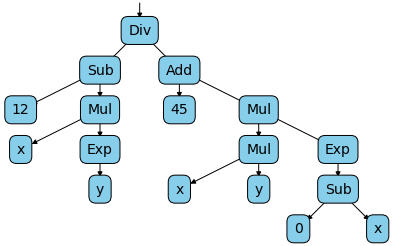
Nous pouvons maintenant facilement calculer la dérivée partielle de z en fonction de x et de y avec le code suivant :
print(z.grad(x)) # T:-3.34729777301069
print(z.grad(y)) # T:-9.70176956641438
Ce qui va générer les deux graphes suivants :
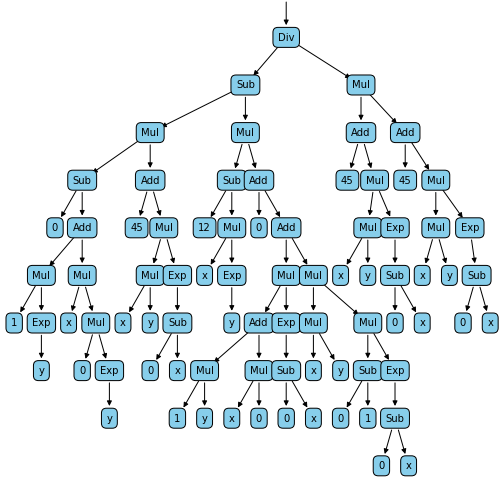
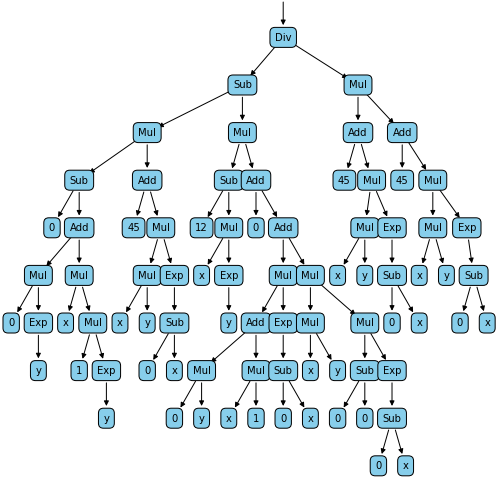
Enfin, pour vérifier que notre système de dérivation automatique fonctionne, nous pouvons comparer le calcul numérique de nos dérivées avec le calcul fait par la bibliothèque Sympy :
import sympy as sym
xs = sym.Symbol('xs')
ys = sym.Symbol('ys')
zs = (12 - (xs * sym.exp(ys))) / (45 + ((xs * ys) * sym.exp(-xs)) )
d = zs.diff(ys)
print(zs.diff(xs).evalf(subs={xs:3, ys:5})) # -3.34729777301069
print(zs.diff(ys).evalf(subs={xs:3, ys:5})) # -9.70176956641438
Le résultat obtenu avec la bibliothèque Sympy est strictement le même qu'avec notre classe Tensor !
Améliorations & Optimisations possibles
Nous venons de créer le système de différenciation automatique le plus simple qui existe, et surement aussi le plus lent. On peut si on le désire rajouter des opérations plus complexes, du moment que l'on sait comment les dériver. En l'état, cette classe ne peut manipuler que des scalaires; pour qu'une telle bibliothèque soit le plus utile, il faudrait rajouter la gestion des opérations sur les tableaux de tailles arbitraires.
Également, en regardant les graphes, on peut constater que certaines optimisations sont possibles :
- Si on est dans un noeud de multiplication et qu'un des deux children vaut 0, on ne devrait pas explorer plus loin. Car on sait que quoique soit multiplié par 0, vaudra toujours 0.
- En parcourant l'arbre pour effectuer une dérivée par rapport à un tenseur x, si on se trouve dans un noeud qui ne dépend pas de x et dont tous les enfants ne dépendent pas de x, on pourrait arrêter le parcours à cette étape et considérer le noeud courant comme une constante. Ce type d'optimisation pourrait grandement améliorer la vitesse de calcul pour des graphes avec beaucoup de noeuds et de variables différentes.
- En regardant le graphe on peut voir que certaines opérations sont répétées. On peut imaginer mettre en place un cache pour ne pas répéter les calculs plusieurs fois.
J'espère que cet article vous a aidé à comprendre la façon dont la différenciation automatique est effectuée pour l'optimisation et l'apprentissage des réseaux de neurones.
N'hésitez pas à me donner votre avis en commentaire.